今回はニューラルネットワークの概念を理解し、Pythonでニューラルネットワーク構造を実装し理解したいと思います。
本記事の目的
本記事は以下を目的としています。
・ニューラルネットワークの概要や活用用途を理解すること
・実際に動かして仕組みを理解すること
ニューラルネットワークとは
ニューラルネットワークは、人間の脳のしくみから着想を得たもので、
脳機能の特性のいくつかをコンピュータ上で表現するために作られた数学モデルです。
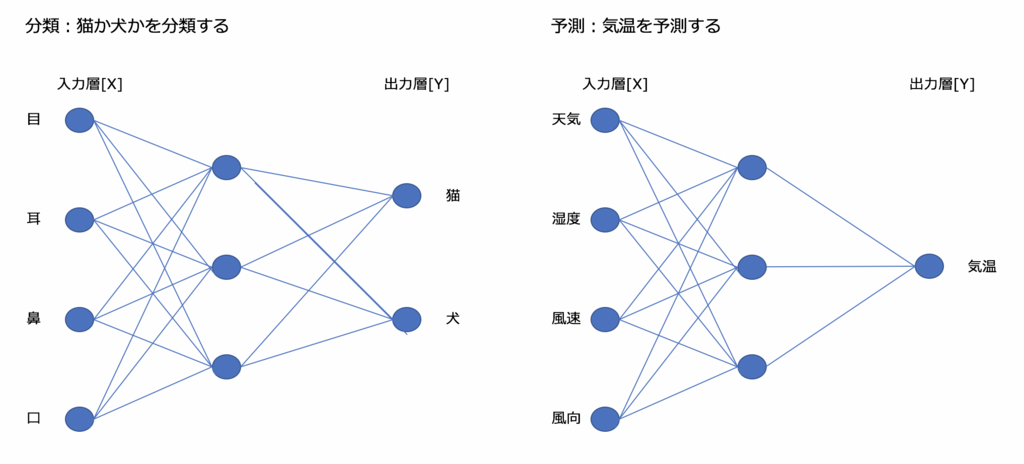
人間でいうと目や鼻・耳から得た情報[X]から判断[Y]を判断します。
今までの歴史を振り返るとニューラルネットワークはは盛り上がりそうで冷めていく波が繰り返されてきた。
しかし、ここ数年、特に2015年以降より急速な盛り上がりを示している。その大きな理由は、速く、比較的安価に、強力な並列処理を実現できる「GPU(Graphics Processing Unit)コンピューティング」の存在だ。
ニューラルネットワークは極めて高い計算処理性能を要することが課題だったが、GPUコンピューティングなどの技術的進歩を背景に、速く、比較的安価に、強力な並列処理を実現できるようになった。
特に画像の分野ではディープラーニングを利用して訓練されたシステムによる画像認識性能が、人間の能力を超えるまでになっている。このような背景からディープラーニングは注目を集めている。
ニューラルネットワークの活用用途
活用用途としては画像認識(画像タグ付け、物体検出、異常検知)
や音声認識でディープラーニングの活用が行われています。下記のような条件が満たされている場合ディープラーニングを行うことができます。
・ラベル付きデータた大量にある
1クラス1000件以上あれば良い結果が得られる。
ただし少ないデータでそれなりの性能を出すことも可能
ニューラルネットワークの学習方法
ニューラルネットワークの学習を理解する。
ニューラルネットワークはとても複雑な関数であるため、直接最適なパラメータを求めることはできません。
トライアンドエラーを繰り返し探索する。
ニューラルネットワークから算出した実際の値と予測値の誤差が最小となる最適なパラメータの探索を行います。
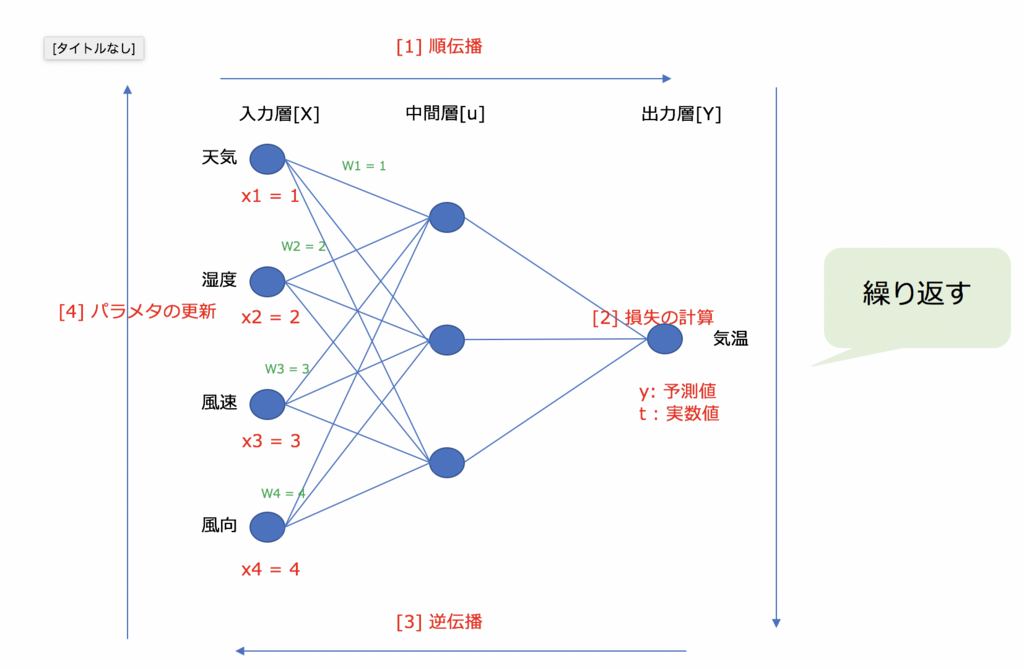
最小となる誤差の探索には微分[傾き]を用いる。
誤差ができるだけ小さくなる予測値[y] が最適なパラメータだと言える。wやbを変更すると誤差[loss]は変化する。
loss(w)の全体像はわからないが、もしwでloss(w)を微分することができればwをどちらに動かせばlossが小さくなるか把握することができる。
微分した値でwを更新しlossが減少しなくなるまで繰り返し行う。
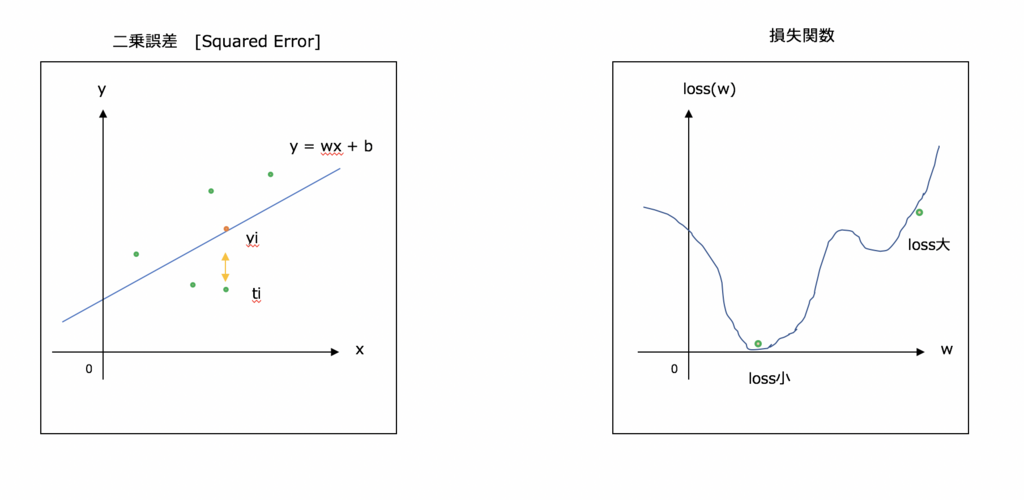
誤差伝播法の概念
誤差逆伝播法と呼ばれるアルゴリズムを活用すると今のパラメータに置ける損失の微分係数(勾配)が計算できる。
今回はこの誤差逆伝播法を用いて画像の分類問題を行います。損失の微分方法としてはRelu関数を用います。
Relu関数を用いて最適なパラメータの計算を行います。
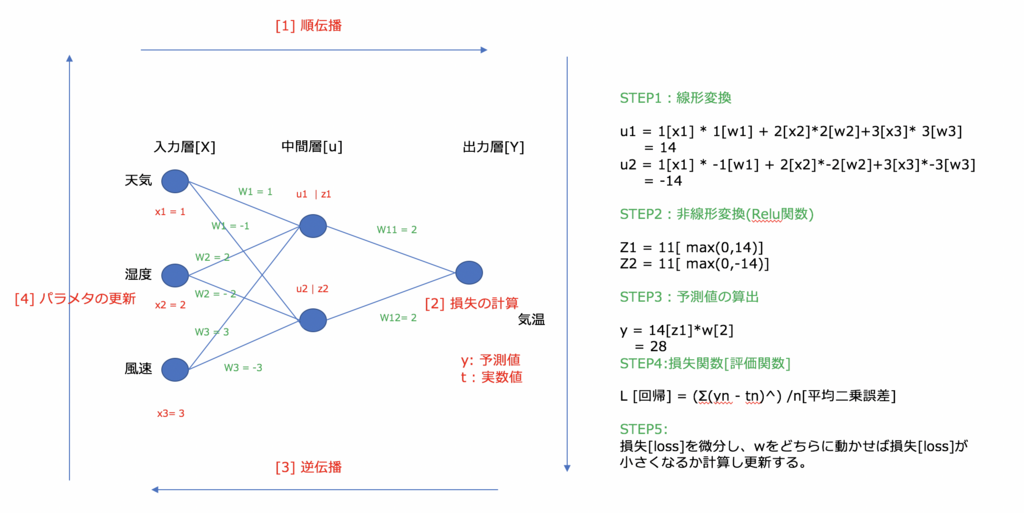
実装編
実際に画像データを用いて識別を行いたいと思います。
STEPに従い、説明変数Xの線形変換、非線形変換、予測値の算出、損失関数の算出、微分[パラメータの調整]で
を行いたいとおもいます。
# ライブラリ import numpy as np import chainer.functions as F import chainer.links as L
# 説明変数[x] np.random.seed(3) x = np.array([[1,2,3]],dtype = 'f')
STEP 1 線形変換
# ニューラルネットワーク:入力層 3 中間層 2 fc = L.Linear(3,2) print("重み:{}".format(fc.W)) print("バイアス:{}".format(fc.W)) u = fc(x) print("線形変換:{}".format(u)) # out 重み:variable W([[ 0.02888694 -0.23364061 -0.31486371] [-0.8928591 0.56717008 -0.63570172]]) バイアス:variable W([[ 0.02888694 -0.23364061 -0.31486371] [-0.8928591 0.56717008 -0.63570172]]) 線形変換:variable([[-1.38298547 -1.66562414]])
STEP 2 非線形変換
z = F.relu(u) print("非線形変換:{}".format(z)) # out 非線形変換:variable([[ 1.70384192 0. ]])
STEP 3 予測値[y]
# 中間層2 出力層1 fc2 = L.Linear(2,1) # 予測 y = fc2(z) print("予測値:{}".format(y)) # out 予測値:variable([[-1.42774189]])
STEP 4 損失関数[loss]
# 教師データ t = np.array([[3]],'f') # 平均二乗誤差の計算 loss = F.mean_squared_error(t,y) print("損失関数:{}".format(loss)) # out 損失関数:variable(19.60489845275879)
全体の流れ
np.random.seed(3) x = np.array([[1,2,3]],dtype = 'f') # 線形変換 fc1 = L.Linear(3,2) u1 = fc1(x) # 非線形変換 z1 = F.relu(u1) fc2 = L.Linear(2,1) # 予測 y = fc2(z1) # 実数値 t = np.array([[3]],'f') # 損失関数 loss = F.mean_squared_error(t,y)
上記を繰り返し損失関数を小さくすることで最適なモデルを構築します。
次は実際にニューラルネットワークを活用し問題を解いてみたいと思います。
case-k.hatenablog.com
参考
「AI」「機械学習」「ディープラーニング」は、それぞれ何が違うのか:「ニューラルネットワーク」とは何か - @IT