代表的確率分布の一つである、ポアソン分布について記事を書きました。ポアソン分布の概要や実際の例題を解きながら理解を深めていきたいと思います。
ポアソン分布とは
「単位時間あたりに平均 λ 回起こる現象が、単位時間に k 回起きる確率」を表すのに使われる確率分布のことです。例えば、地方に東京からくる人は、年間[単位時間]で5人[ λ]とします。このように単位時間あたりに、限りなく数が少ないデータはポアソン分布に従い、ポアソン分布で確率を求めることが可能です。上の例では、「地方に東京からくる人は、年間[単位時間]で3人[ k]回起きる確率」を求めることが可能です。
特徴としてはカウントデータは0以上の整数値しか実現値として得られないという特徴があります。これは-∞ ~ +∞の実数を取りうる正規分布とは大きな違いです。ポアソン分布の母数は強度λのみです。ポアソン分布に従う確率変数はその期待値も分散もλとなります。サンプルサイズ[n]が十分に大きく、確率[p]が非常に小さいとき、np=『一定』と考えることができます。そこでnp=λとおくと事故が起こる回数はポアソン分布に従うということができます。
例題
1年間で飛行機が墜落する確率について考えます。飛行中の飛行機10,000,000台に1台の割合で飛行機が墜落する場合、p=0.00000001です。1年間(n=365)で事故が起こる確率を確率変数Xとすると2回[k回]事故が起こる確率を求めよ。
mu = 365*0.00000001 # λ = n*p k = 2 # 発生回数 p = sp.stats.poisson.pmf(k=k,mu = mu) print(p) print("poisson prob:{:.20f}".format(p*2.7182818)) # out put 6.661225686481895e-12 poisson prob:0.00000000001810708855
ポアソン分布図示します。
# λ=muのポアソン分布 poisson = sp.stats.poisson(mu=mu) # 乱数 np.random.seed(1) rvs_poisson = poisson.rvs(size=365) # 確率質量関数 m = np.arange(0,10,1) pmf_poisson = poisson.pmf(k=m) sns.distplot(rvs_poisson, bins=m, kde = False,norm_hist = True,color = 'gray') plt.plot(m, pmf_poisson, color='black')
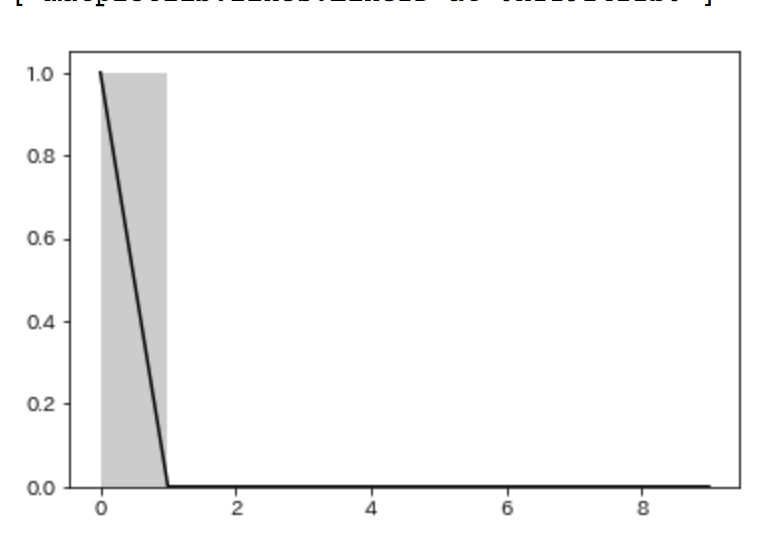
二項分布とポアソン分布の関係
上記の問題は二項分布の公式に当てはめることができます。
二項分布については以下を確認してみて下さい。
case-k.hatenablog.com
n = 365 x = 2 p = 0.00000001 bp = comb(n,x)*p**x*(1-p)**(n-x) print(bp) # 「e」は「ネイピア数」あるいは「自然対数の底」と呼ばれる定数で、「e=2.7182818...」という無限に続く値をもちます。 print("binomial prob:{:.20f}".format(bp*2.7182818)) # out put 6.642975885953526e-12 binomial prob:0.00000000001805748045
二項分布を図示します。
binomial = sp.stats.binom(n=n, p=p) np.random.seed(1) data_binom = binomial.rvs(size=365) # 確率質量関数 m = np.arange(0,10,1) pmf_binomial = binomial.pmf(k=m) # 乱数のヒストグラムと確率質量関数を重ねる sns.distplot(data_binom, bins = m, kde = False, norm_hist = True, color = 'gray') plt.plot(m,pmf_binomial, color = 'black') plt.ylabel("binomial probability") plt.xlabel("random variable")
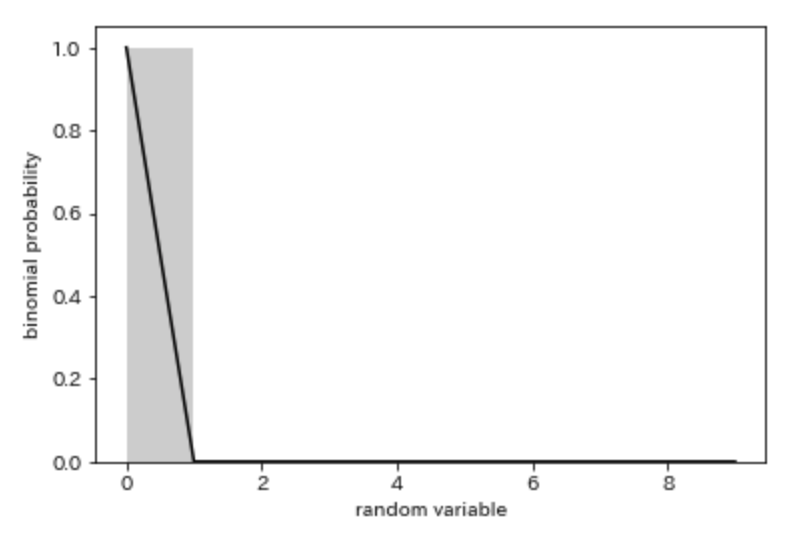
二項分布はnが十分に大きく、pが小さいとポアソン分布に近似することが確認できます。
ポアソン分布の場合Nを無限に増やしても正規分布になることはないので中心極限定理は活用できません。
中心極限定理に関してはこちらを確認してみて下さい。
case-k.hatenablog.com
参考:
ポアソン分布とは何か。その性質と使い方を例題から解説 【馬に蹴られて死ぬ兵士の数を予測した数式】 | アタリマエ!