この記事では説明変数3つ以上の偏相関係数算出方法をPythonで行います。実際のコードはこちらにあげておきます。
# partial_correlation_coefficient.ipynb
# Partial_correlation.csv
github.com
偏相関係数とは
偏相関係数とは変数間の交互作用を取り除いた純粋な相関係数と言えます。
多変量である場合、個々の説明変数が互いに相関している場合が多いかと思います。説明変数間で相関していると目的変数に対し実際には相関していないのに、相関しているように見えてしまいます(疑似相関)。偏相関係数とは説明変数間の影響を取り除いた純粋な相関係数と言えます。
偏相関係数についてはこちらの記事がよくまとまっていました。
bellcurve.jp
この記事の背景
多変量データの偏相関係数を出そうと調べたところ、ほとんどが2変数の偏相関係数の算出する記事ばかりでした。
実際に多変量解析を行う場合は、2変数以上の場合が多いかと思います。調べていたところ、3変数以上の偏相関係数の算出方法を記載した記事を見つけたので、実際にPythonで実装し、正しい偏相関係数が求められたか検証してみました。
3変数以上の偏相関係数算出方法
説明変数が3変数以上の場合の偏相関係数算出方法です。
1.相関行列の逆行列を求める
2.逆行列の各要素を2つの対角要素の積の平方根で割り,符号を逆転する
www.fujiitoshiki.com
実装偏
実際に上記の方法をPythonで実装してみたいと思います。データはこの後の検証も兼ねてこちらの記事のデータを参考とさせて頂きました。
tjo.hatenablog.com
偏相関係数と検証はこちらの記事を参考にさせて頂きました。
blog.goo.ne.jp
データはこちらを活用してください。広告のCVと相関のあるカラムを調べます。
github.com
cv_data = pd.read_csv("./data/Partial_correlation.csv")
cv_data.head()

目的変数を2値に変換します。
def conv_dummy(x): if x == "No": return 0 else: return 1 cv_data["cv"] = cv_data["cv"].apply(lambda x : conv_dummy(x)) cv_data.head()
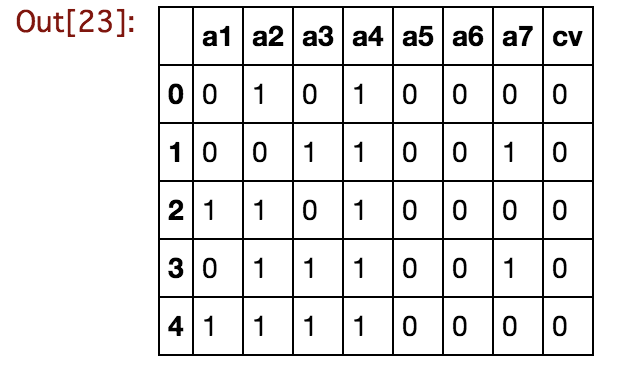
3変数以上の偏相関係数を求めてみます。3変数以上の偏相関係数算出方法にしたがって、関数を定義します。
# 偏相関係数 def p_corr(y,data): corr = data.corr() #1.相関行列の逆行列を求める inv_corr = pd.DataFrame(np.linalg.inv(corr),columns=corr.columns,index=corr.columns) p_corr_list = [] #2.逆行列の各要素を2つの対角要素の積の平方根で割り,符号を逆転する for x in corr.columns: p_corr = -(inv_corr[x][y] / np.sqrt(inv_corr[x][x]*inv_corr[y][y])) p_corr_list.append([x ,p_corr]) return p_corr_list
実際に偏相関を求めてみます。
# 目的変数 y = "cv" cv_data = pd.read_csv("./data/Partial_correlation.csv") cv_data["cv"] = cv_data["cv"].apply(lambda x : conv_dummy(x)) cv_data=p_corr(y, cv_data) cv_data

検証
算出結果が正しいか検証してみます。こちらの記事で同じデータを活用して2変数間の偏相関係数を算出していたので、検証結果が正しいか確認してみます。
blog.goo.ne.jp
a1 a2 a3 a4 a5 a6 a7
a2 -0.027
a3 -0.005 0.003
a4 -0.005 0.012 0.019
a5 0.027 -0.007 -0.025 0.015
a6 -0.031 -0.013 0.018 -0.020 0.015
a7 0.006 -0.029 -0.031 0.007 -0.003 -0.011
cv 0.112 -0.059 0.003 -0.284 0.176 0.807 0.006
計算結果が一致しました。どうやら問題なさそうです。