最小二乗法の傾きが0でないことをPythonでt検定してみた

データを分析して実際に偶然ではなく本当に確からしいのか確かめる方法として仮説検定があります。仮説検定とはある仮説に対して、本当にそれが確からしいか調べるための統計学手法です。
今回は仮説検定の1つである1変量データに対するt検定[両側]で問題を解きます。

記事の目的

この記事は以下を目的にしています。
・t検定の概要理解
・t検定を活用して実際に統計検定をしてみる
・統計用語の理解

t検定とは

母平均を検定するための手法です。例えば標本サンプルから算出したデータの平均値から、母平均が0と異なることを確かめるために利用します。
良い点としては母分散が未知の場合に適用できることです。

1変量データのt検定とは

1変量データのt検定の特徴を簡単に述べます。
・対象：平均値
・判断すること：平均値が"ある値"と異なると言えるかどうか
例えば、中学1年生の男子身長の平均が160cmか確かめたいとします。しかし、158cmの人もいれば163mの人もいます。
身長には多少ばらつきはありますが、平均は160cmであって欲しいです。
こんなときt検定を活用すれば、「中学1年生の男子身長の平均が160cmと異なっているかどうか」判断することができます。

t検定の前提条件

t検定を使うためには、対象となるデータが「正規分布」とうい確率分布に従っている必要があります。正規分布に従っていない場合、「一般化線形モデル」などを活用する必要があります。正規分布に従っていることを前提に説明させて頂きます。

※　jupyter notebookを活用を前提とします。

サンプルデータの準備と可視化

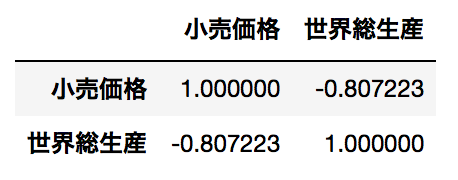
1991年から2015年までの各年における日本の1ポンドあたりの小売価格を縦軸に、前年の世界のコーヒー総生産を横軸としたデータを用意し、散布図で可視化します。

#　ライプラリ
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline

from sklearn import linear_model
from scipy.stats import norm  
from scipy.stats import t 

#　サンプルデータ
columns = ["小売価格","世界総生産"]
data_df = pd.DataFrame()
data_df["小売価格"] = np.array([15.5,15,18,12,14,13,13,12,9,16,8,8,9,8,9,9,6,8,13,6,8,8,3,4,6])
data_df["世界総生産"] = np.array([87,90,91,91,100,100,100,100,105,110,110,112,113,118,122,122,128,129,130,135,140,147,148,149,150])
data_df.head()

#　散布図
X = data_df[["世界総生産"]] 
y = data_df[["小売価格"]]
plt.scatter(X,y)
plt.xlabel("世界総生産")
plt.ylabel("小売価格")

相関係数の確認

data_df.corr()

負の相関が高いようだ。

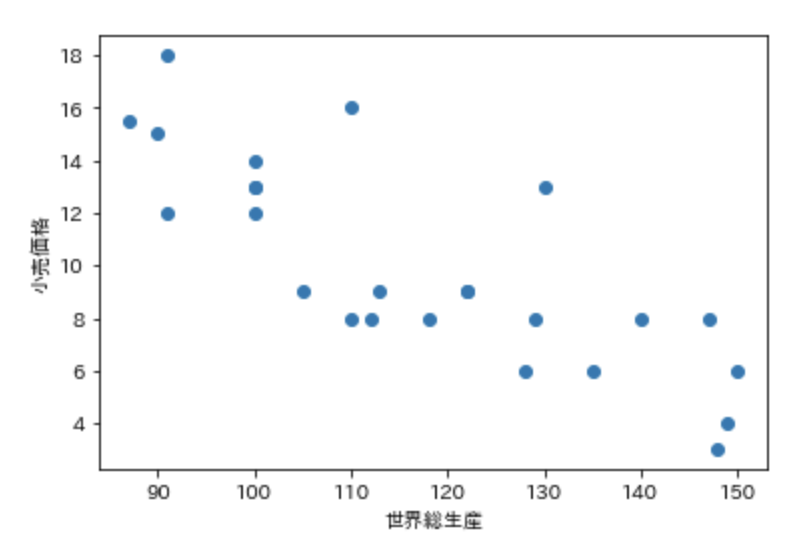
最小二乗法で傾きを確認

最小二乗法とは残差の二乗の和を最小にしたものです。
残差とは各点から垂直な線を近似直線まで引いたものであり、残差の合計が最小となる直線を求めます。

y_reg1 = linear_model.LinearRegression()
y_reg1.fit(X, y)
plt.scatter(X,y)
plt.xlabel("世界総生産")
plt.ylabel("小売価格")
plt.plot(X, y_reg1.predict(X), color='red')
print("傾き：{}".format(y_reg1.coef_)) 
print("切片：{}".format(y_reg1.intercept_)) 

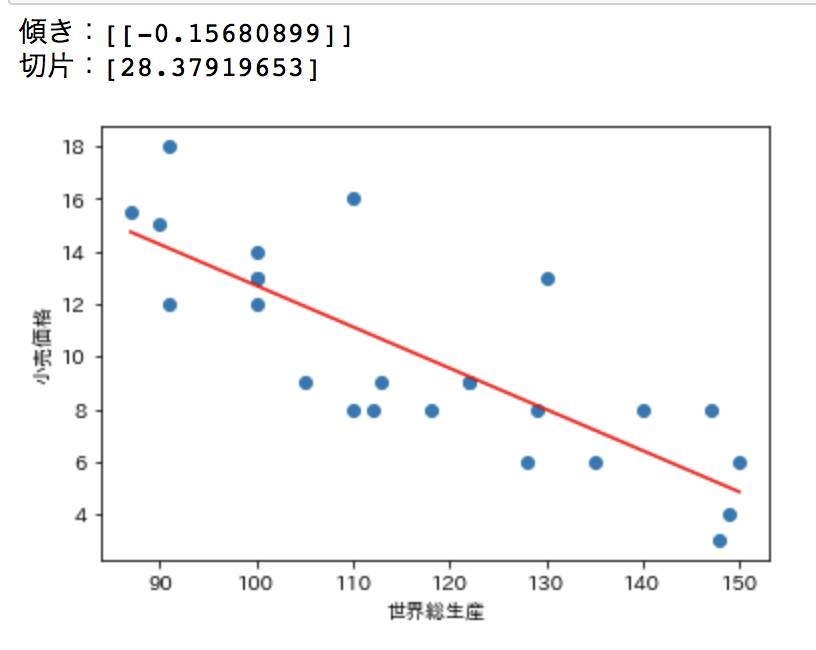
残差を可視化

最小二乗法で求めた回帰直線と実際のデータとの残差を可視化します。
可視化した赤い直線と青いデータの距離が残差となります。

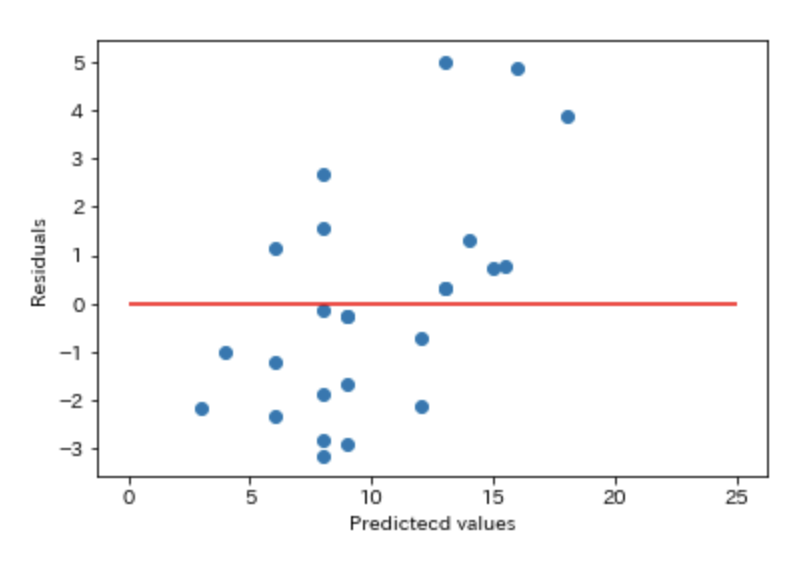
# 残差
residual = y - y_reg1.predict(X)
# 残差を図示
plt.scatter(y , residual)
plt.xlabel('Predictecd values') 
plt.ylabel('Residuals')
plt.hlines(y=0, xmin=0, xmax=25, color='red')

仮説を立てる

仮説を証明するために、否定したい仮説(帰無仮説)と肯定したい仮説(対立仮説)を立てます。
帰無仮説：母平均の傾きは0である(μ=0)
対立仮説：母平均の傾きは0ではない(μ!=0)
上記のような仮説の立て方を両側検定といいます。
両側検定と片側検定の使い方は検証したい内容によって異なります。
(例)
薬A中の成分Bの含有量は100mgではない[両側検定　μ != 0 ]
→　成分Bの含有量が100mgかどうかを調べるための検定
薬A中の成分Bの含有量は100mgより多い[片側検定　μ > 0 ]
→　成分Bの含有量が100mgより多いかどうかを調べるための検定
薬A中の成分Bの含有量は100mgより少ない[片側検定 μ < 0 ]
→　成分Bの含有量が100mgより少ないかどうかを調べるための検定

今回検定したいことは母平均の傾きが0でないことであるため両側検定となります。母平均の傾きが0という帰無仮説の下で、t値を算出し、t値が95%信頼区間外にあった場合帰無仮説を棄却し、対立仮説を採用します。

標準偏差・標準誤差・自由度・t値算出

t検定を行うためには帰無仮説から算出したt値とt分布の信頼区間を算出するための自由度が必要となります。
t値 = 標本平均[x mean] - 母平均[μ] / 標準誤差[se]
se = 不偏標準偏差[s] / √サンプル数[n]
不偏標準偏差[s] = √(残差の二乗合計値 / (n - 1))
(残差の二乗合計値をサンプル数-1で割った値の平方根)

自由度[N] = サンプル数[n] -2[α:傾き、β:切片]
自由度は最小二乗法で推定したパラメータの数(α:傾き、β:切片)をサンプル数から引いた値となります。

# サンプル数
n = len(X)
print("sample count：{}".format(n))
# 自由度
N = n - 2 
print("degree of freedom：{}".format(N ))
# 不偏分散
V = np.sum(np.square(np.array(residual))) / (n - 1)
print("variance：{:.5f}".format(V))
# 不偏標準偏差
std =  np.sqrt(V)
print("standard division：{:.5f}".format(std))
# 標準誤差
se = std / N
print("standard error：{:.5f}".format(se))
# t値
t_value = (y_reg1.coef_ - 0) / se
t_value = (-0.807223 - 0) / se
print("t value：{:.2f}".format(t_value ))

# out 
sample count：25
degree of freedom：23
variance：5.33097
standard division：2.30889
standard error：0.10039
t value：-8.04

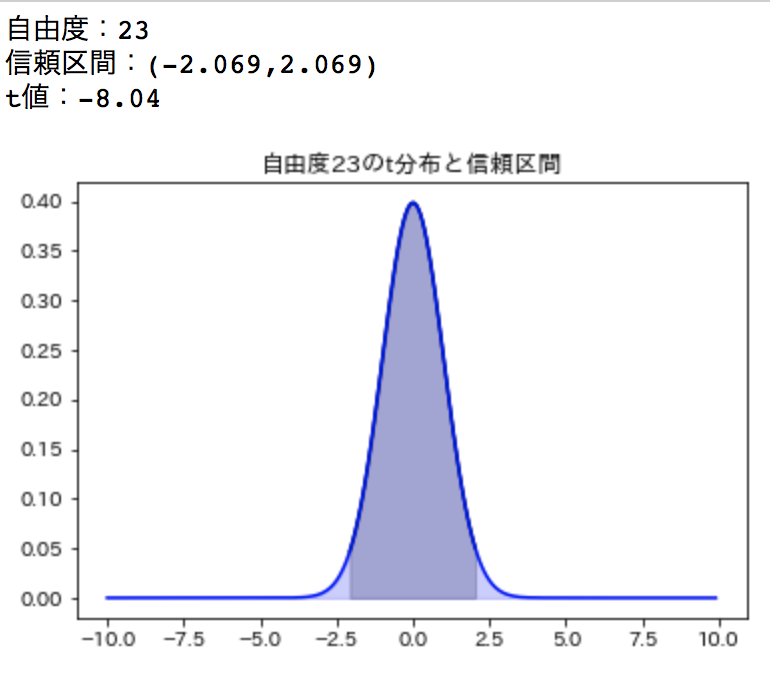
自由度23のt分布を可視化・95%信頼区間を求める

# 信頼区間：t分布表　両側検定,  95% , 自由度　N 
alpha = 0.95
intervals = t.interval(alpha=alpha, df=N)
print("自由度:{}".format(N))
print('信頼区間:({:.3f},{:.3f})'.format(intervals[0],intervals[1]))
print('t値：{:.2f}'.format(t_value))

# t分布　信頼区間
x = np.arange(intervals[0], intervals[1], 0.1)
y = norm.pdf(x=x, loc=0, scale=1)
plt.plot(x, y, 'black')
plt.fill_between(x, y, color='black', alpha=0.2)

x = np.arange(-10, 10, 0.1)
# 平均0、標準偏差１の正規分布から入力データの確率を得ている
y = norm.pdf(x=x, loc=0, scale=1)
plt.plot(x, y, 'b')
plt.title("自由度{}のt分布と信頼区間".format(N))
plt.fill_between(x, y, color='b', alpha=0.2)
plt.show()

t検定で帰無仮説を棄却

真の傾きが0という帰無仮説の下のt値-8.04は、自由度23のt分布に従います。このt値は95%信頼区間-2.069 ~ 2.069外にあるため棄却されます。

t値からp値を求める。

P値の計算方法
両側検定を行うことを前提としてP値の計算を行います。今回の標本から計算されたt値のことをt標本と呼ぶことにします。
母集団が正規分布に従うと仮定すると、t値はt分布に従うと考えられるため、t分布の累積分布関数が使えます。

t検定におけるp値の役割としては帰無仮説[傾き 0]に基づいたt値の値が、t標本より大きいことを確率的に算出し、
t分布の累積分布関数を活用すると「母平均を0と仮定した時に、t値がt標本を上回る確率」を計算することができる。
この確率を計算することができます。
p値は下記のように計算されます。

p値 = (1-α)*2

最後に*2をしているのは両側検定だからである。傾きが0とは異なる確率を計算するには、傾きが0より大きい場合と小さい場合があるからです。片側検定の場合は0より大きいか、小さいかのどちらかなので単に1-αがp値となります。

# t値から負の符号を取り除く
alpha = stats.t.cdf(np.abs(t_value), df = N)
p = (1-alpha)*2
print("{:.9f}".format(p))

# out put
0.000000039

p値が0.000000039となりましたので、傾きが0である確率は限りなく、
小さいことがわかり、帰無仮説を棄却することができます。

所感

今回は1変量データのt検定を実施してみました。
実際の課題に対しても適用させて、統計学視点からどうか考える習慣をつけていきたいと思います。
統計検定2級の本読んでるのですが、実際にこうやって課題設定して行うと、身について来る気がします。
ちょっと感覚的ですけどね(笑)

以上が両側t検定となります。

参考サイト
24-1. 母平均の検定（両側t検定） | 統計学の時間 | 統計WEB