代表的な確率分布として正規分布や二項分布、ポアソン分布があります。本記事では二項分布と正規分布の関係性について、実際にPythonで例題を解きながら理解していきたいと思います。二項分布については以下よりご確認ください。
case-k.hatenablog.com
二項分布と正規分布の関係性
二項分布は正規分布に近似させることができます。二項分布の正規近似させる定理を「ド・モアブル–ラプラスの定理」と言われており、二項分布 Bin(n,p)は n が十分大きいとき,平均 np,分散 np(1−p)の正規分布に近づく特性があるのです。二項分布を正規分布することや、わざわざ近似させるメリットを書きたいと思います。
例題
実際にPythonで例題を解きながら、二項分布が正規分布に近似することを理解したいと思います。
例題(1)
クリック率が0.2の広告Aがある。広告Aを1000回表示させ、500回クリックさせる確率を求めよ。
この例題は広告がクリックされたか、されないかの二択であるため、二項分布を適用することができます。
n = 1000 x = 300 p = 0.3 bp = comb(n,x)*p**x*(1-p)**(n-x) print("binomial probabilty:{:.3f}".format(bp)) # out put binomial probabilty:0.028
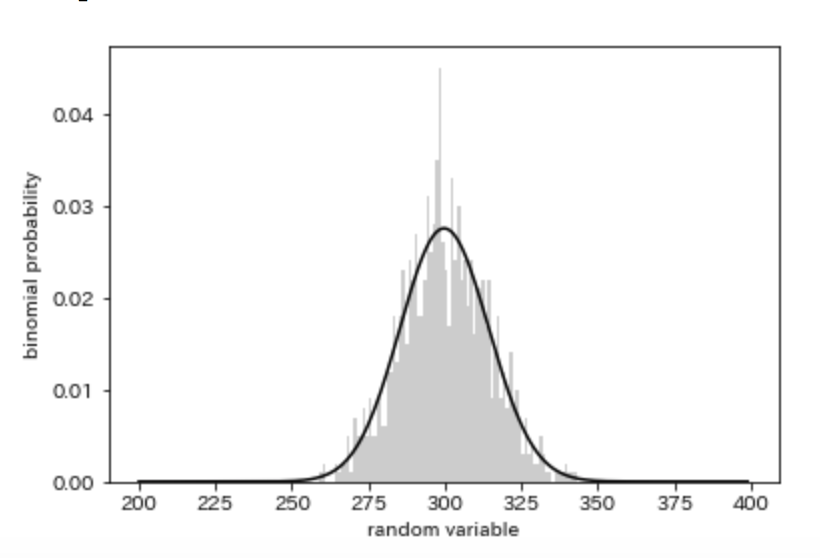
binomial = sp.stats.binom(n=n, p=p) np.random.seed(1) data_binom = binomial.rvs(size=1000) # 確率質量関数 m = np.arange(200,400,1) pmf_binomial = binomial.pmf(k=m) # 乱数のヒストグラムと確率質量関数を重ねる sns.distplot(data_binom, bins = m, kde = False, norm_hist = True, color = 'gray') plt.plot(m,pmf_binomial, color = 'black') plt.ylabel("binomial probability") plt.xlabel("random variable")